(圖片素材取自網路免費圖片。)
投資為何需學習貝氏定理?
貝氏定理(Bayes' theorem)是在機率論中非常重要的一條定理,國內的高中數學課程就已經學到了,只不過台灣教育比較速成,大多只是應付考試而已。因此,也許您已經學過了,但筆者估計至少 9 成以上的人們忘了或從來沒有會過,本文將帶您重新複習一下「貝氏」,以及如何運用貝氏定理來調整投資的加減碼策略。
「貝氏定理」的數學式表示很簡單,但是其實意含一點都不簡單,因此本文下方會有一點點稍微複雜的數學式說明,如果看得有點吃力建議就先跳過不理,等後面文字敘述及結論看完後,若您真的很有興趣再回頭來研究吧。
為什麼要學習貝氏理論呢?在投資裡,我們面對的情況其實大多都是充滿不確定性,但我們面對未知的領域時往往就是靠著「直覺」在行動。不幸的是,「直覺」是非常脆弱且不可靠的東西,尤其是在「投資」裡更是反指標。因此,學習貝氏理論後,第一件事就是要讓我們明白為何我們的「直覺」跟「事實」差很大;等到更熟練的掌握了貝氏思考後,您在看待投資的這件事上,以及面對更多未知的領域裡,思考的方式就會變得很不一樣。
投資裡,常有一句話,「會買的是徒弟,會賣的才是師傅」。因此,「資金控管」是我們最可以掌握的因素,該怎麼將資金依據現有的證據做適當的加減碼?當你真正理解了貝氏定理後,掌握了貝氏的思考準則後,就可以馬上脫離「還沒回到成本」、「資金套牢」、「放著看還能不能漲更多」、「不賣就不算賠」等等影響投資的心理魔障,從「徒弟」快速的晉升為「師傅」。
說到底,投資唯一的聖杯就是我們應該將資金放在有比較高勝率,可創造財富的地方,並且將錢從賠錢的錢坑裡拿回來,由於人性風險趨避及不願誠實面對虧損的弱點讓我們無法擁有貝氏思考。看完本篇,讓您從現在起學會利用貝氏定理,讓資金在最高勝率下滾動成長,進而創造穩定的現金流。
貝氏定理解說
條件機率與貝氏定理
本節我們即將正式進入到貝氏理論,首先我們要將「條件機率」與「貝氏定理」一起講,原因是這兩個式子其實是互為對稱的,貝氏定理就是條件機率因果顛倒的反寫。
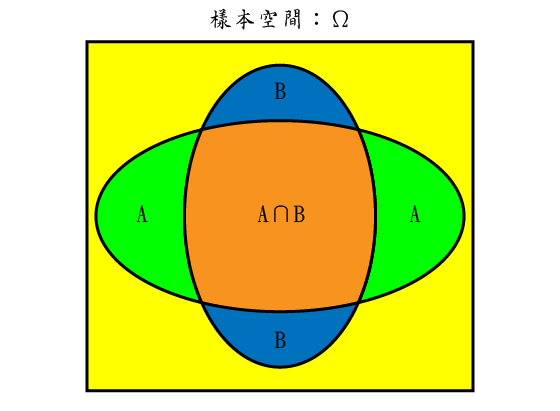
條件機率就是指一個事件(假設為 B)在另一事件(假設為 A)已經發生的情況下所可能發生的機率,數學符號是記為 P(B| A),而聯合機率 P(A∩B) 則是指事件 A 與事件 B 共同發生的機率。完整的條件機率數學式及幾何圖形表示如下:
`"P(B|A)"=frac{P(A nnn B)}{P(A)}`
(兩事件 A、B 發生,聯合事件 A∩B 發生的幾何表示,自行繪製。)
因此,條件機率應用在以「統計」為基礎的情況下,可以透過事件 A、事件 A∩B 發生的次數,經由事前機率 P(A)、P(B|A)發生的情況下,以得到聯合機率 P(A∩B)。因此,在事後機率 P(B) 無法掌握,但確實發生事件 B 的情況下,透過已知的情報反推計算 P(A|B) 就是貝氏定理。
反果為因的貝氏定理
由先前的條件機率,事前已知的機率可以透過「統計」或「主觀經驗」等假設,得到 P(A)、P(A')、P(B|A)及 P(B|A')等等,在 P(B)為未知的情況,但事件 B 已發生的前提下去計算 P(A|B) 的機率,就是如下的貝氏定理。
`P(A|B)=frac{P(A nnn B)}{P(B)}=frac{P(B|A)P(A)}{P(A nnn B)+P(A' nnn B)}`
`=frac{P(B|A)P(A)}{P(B|A)P(A)+P(B|A')P(A')}`
上述所說的 P(B|A') 代表的是在事件 A 沒有發生的情況下,而事件 B 發生了。也就是說,在投資裡仍有一部份因素是我們無法掌握的,但只要掌握越多的事件 A,就可以更精確的預測事件 B 發生的概率。而事後機率 P(A|B) 便可以用來修正我們事前機率的預估值,或推估還沒有觀察到的現象。
貝式定理在投資理財上的應用
看完上述一節,相信有很多人都是「霧煞煞」,不要緊,這節就跟大家說明上節與理財投資的對應關係。首先「事件 A」我們可以定義為各種資訊,比如:「公告營收數據」、「新聞訊息」、「上下游出貨量」、「財報資料」、「內外資法人進出」、「券資比」等等;而「事件 B」就很單純,只需要定義一個,就是我們最關心的「股價的漲跌」。因此事件 A 的機率 P(A) 就是我們假設的事前機率,如「營收是否可以持續的機率」、「內外資持續買進的機率」、「券資比達到軋空的機率」、「財報數據合乎預期的機率」、「上下游產品出貨穩定的機率」。而 P(B|A) 就是我們的從「經驗上得到的機率」或「統計數據得到的機率」,如「營收數據不佳造成股價跌的機率」、「上下游出貨量減少影響該公司股票的機率」、「內外資法人轉買或轉賣造成股價上漲或下跌的機率」,「出現重大訊息造成股價上漲或下跌的機率」等等。
而貝氏推論中的 P(A|B)即是股價漲跌事件 B 已經變化的情況下,推估由未知事件 A 造成的機率,由於股價往往跑在前面,如在還沒有公布營收或財報的情況下股價率先反應,從股價的動作可以反向的推估未知事件 A 發生的可能性。
因此,我們可以知道,影響股價漲跌的因素很多,比較有概念的讀者可能發現了,事件 A 往往並非是單一事件,而是多個事件所組成的機率分布,下面就討論多條件機率下的貝氏定理。
多條件機率下的貝氏定理
貝氏定理的應用大部份情況下都在多條件機率下所產生,先假設兩個事件 A1、A2 發生為前提的情況下,事件 B 發生的機率,且 A1 與 A2 互為獨立,共有兩個條件機率如下:
`"P(B|A1)"=frac{P(A1 nnn B)}{P(A1)}`
`"P(B|A2)"=frac{P(A2 nnn B)}{P(A2)}`
(兩事件 A1、A2 發生,事件 B 發生的情況,自行繪製。)
貝氏定理計算「反果為因」的情況,在多條件情況下,已知機率 P(B)發生的情況下,如何計算 A1 發生的機率 P(A1|B)?以及 A2 發生的機率 P(A2|B)?在這個情況下,P(B) 變成為已知的事前機率,而 P(A1|B) 及 P(A2|B) 變成事後機率。
`P(A1|B)=frac{P(A1 nnn B)}{P(B)}`
`=frac{P(B|A1)P(A1)}{P(A1 nnn B)+P(A2 nnn B)+P((A1 uuu A2)' nnn B)}`
`={P(B|A1)P(A1)}//{P(B|A1)P(A1)+P(B|A2)P(A2)`
`+P((A1 uuu A2)')P((A1 uuu A2)') nnn B)}`
`P(A2|B)=frac{P(A2 nnn B)}{P(B)}`
`=frac{P(B|A2)P(A2)}{P(A1 nnn B)+P(A2 nnn B)+P((A1 uuu A2)' nnn B)}`
`={P(B|A2)P(A2)}//{P(B|A1)P(A1)+P(B|A2)P(A2)`
`+P((A1 uuu A2)')P((A1 uuu A2)') nnn B)}`
進階應用:貝氏網路
接上述的多條件機率的貝式定理,理想上,當有多事件 A1~An 發生,各自獨立且互斥時,且假設 n 個事件已能充份表達影響漲跌的成份時,可得如下的貝氏定理。
`P(Ai|B)=frac{P(B|Ai)P(Ai)}{P sum_(n=1)^i P(B|Ai)P(Ai)}`
(多事件 A1~An 發生,事件 B 發生的情況,自行繪製。)
當事件 A1 到事件 An 影響股價漲跌的權重都被衡量出來之後,便可以透過演算法來做漲跌預測與決策分析,形成一個貝氏網路,為貝氏定理的進階應用。
(由多事件 A1~An 發生,來判斷買賣決策的貝氏網路,自行繪製。)
舉例:貝式定理的應用
本文中為了讓讀者了解貝氏定理,上述的數學式一律採用高中數學的表示法,不過筆者寫到這邊往回看一下,覺得數學式太多可能還是讓人眼花撩亂,因此再舉 2 個貝式定理的例子如下。
例一:停班課
去年的新聞,7 月 10 日瑪莉亞颱風襲台,柯文哲等到晚間 10 點才宣告正常上班上課,跟新北市及桃園市不同調,讓網友戲稱是否是協商破局的結果。隔日柯文哲說明當時做決定的依據,便是利用「貝氏定理」做出最佳的判斷,當下便讓原本不太領情的網民紛紛閉嘴,同時也拉高民調支持率。
(網路範例,加入溼度的條件機率,可使得天候的估算更為精確,範例取自 https://www.youtube.com/watch?v=evQUrkXNAPg。)
例二:海面搜救
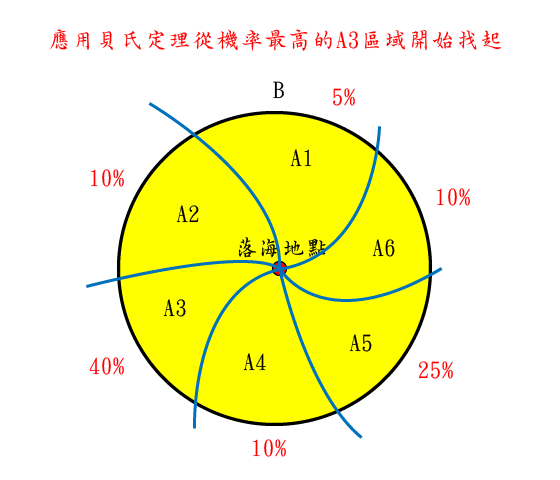
2017 年 11 月新聞為例,幻象 2000 在海域上消失,海巡總局派出人員進行海面搜救。在還沒有運用貝氏定理的情況下,假設落海處如下圖標示的點,在未引入任何資訊的情況下,事前機率 P(B)是平均分布在以落海為中心的一定範圍內。但是假設落引入海流等因素條件下時,將圓形範圍的四週依據海流條件來推估,假設推測結果為 P(A3∩B)=0.4 ,則從這一個區塊開始找起,可以大大的提高搜救的機率。
(海面搜救時,可以根據海流等條件機率的引入優先尋找機率最高的範圍,自行假設與繪製。)
小結
讓我們再次回到投資理財上,股價的漲跌在沒有引入任何數據的情況下,我們可以預估事前機率 P(B) 大致就跟投擲硬幣相差無幾,但是當引入了新的條件之後,經由各種條件機率的計算,不同的股票將產生高低不同的報酬機率 P(B,A1,...,An),只要運用得宜可以大賺小賠。最後再重複一句,「學會了貝氏思考的方式,即掌握了決定勝率的方程式。」
本文可能艱澀難懂,但如果觀念通了,不需任何數學式也能靈活運用貝式思考。文中所有關於機率的定義,其實很大一部份都在於主觀上的假設,然後再透過貝氏定理方法不斷的與新證據進行修正。因此,關於貝氏定理的方法裡,機率的估算是最困難的一部份,而要修正到合乎實際機率的概率更要透過不斷的實驗再實驗。就好比丟銅板的實驗,如果有個人想證明一枚銅板的正反面機率真的是各 0.5,則他就需要不斷的丟,丟到上萬次、上千萬次,才能比較確定銅板的機率是各 0.5。但真實情況是,如果真的要進行這個實驗,且不斷實驗到無限次,每一枚硬幣都不會是機率各半,因為硬幣的邊緣只要不太公正,兩面的重心不太相同,最終結果絕對不會是機率各 0.5,這就是貝氏思考要告訴我們的原則,原則就是我們可以先假設與估算一個合理的機率,然後不斷的用新收到的事實去修正我們原先的預測。因為在「大數法則」下我們知道結果可能會逼近 0.5,但在「強大數法則」下透過更多的實驗,我們就可以得到硬幣上面因為物理瑕疵所造成的微妙差別。
補充:本文上方曾提到貝氏網路,不過在實用上貝氏網路適合在條件參數較少的情況下才有可能計算的出來。另一個跟貝氏網路相似的應用叫做馬可夫鍵,可用來處理「隨機漫步」問題,例如從現在起走 N 步會達到什麼狀態,透過隨機概率去計算可能達到的終值是什麼,相關應用非常強大。
※本文為個人研究,非投資建議,相關數據係依當時公布之財報資料推估,僅供讀者參考。

資金面































0 意見:
張貼留言