(圖片取自網路開放資源。)
前言
在理財投資裡成功方法有千百種,不管您使用的方法是哪一種?但從數學上觀察,一定都符合本文所探討的三種趨勢,可以用「鞅」的這個概念來說明。基本上投資理財不一定需要用到多少數學,但簡易的計算(如簡單加減乘除)卻是必須的,當您沒有投資的任何基礎時,透過數學來理解「投資成功」所需要的要件,可以少走很多冤枉路,也可以建立自己獨立思考的能力。比如說我們面對一件事實,從事件的陳述上常常帶有很多情感的要件,讓自己失去客觀的判斷能力。但若從數學的角度上陳述,就會相對清楚許多,讓自己變得更客觀,也不容易受到外部情勢及個人情緒的干擾。在投資的世界裡,兩個投資技巧差異不大的 A、B 兩個人,可能因為心理素質的不同,而讓投資績效差距拉大。投資是一門商業理論結合機率學、心理學的賽局,因此本文我們就從數學上來探討這個賽局要如何推導吧!
衡量投資的優劣:「鞅」
在開始討論投資方法之前,我們來談一種衡量投資決策績效的概念:「鞅」(Martingale)。「鞅」原本是 18 世紀流行於法國的一種投注策略,當時流行的投資策略邏輯非常簡單,稱為加倍賭注法(也就是現在俗稱的攤平法)。以投擲硬幣的賭局(1 賠 1)來說,若硬幣正面朝上則贏得賭金,反面朝上則失去賭金,而加倍投注的概念,就是當賭徒的財產可以接近無窮時,且賭局也可以無限的持續下去,則贏得賭注的機率會趨近於 1。加倍賭注法看似是一種必然贏錢的策略,但是現實情況是隨著每一次的加倍賭注,賭金的金額呈現指數式的放大,使用這個策略最終都會導致賭徒破產。
後來「鞅」的概念,在 1934 年及 1939 年先後由保羅·皮埃爾·萊維(應用於離散定理)、以及約翰・維爾(應用於連續定理)將相關理論利用數學進行證明,主要的動機是為了表明成功的投注策略並不存在。而後,從 1970 年後,「鞅」就被純粹數學應用在更多領域中進行廣泛的討論,如解決物理上的數學問題(如布朗運動)、金融世界的計量模型(如隨機漫步理論)或博奕理論等等。目前「鞅」的最簡單表示方法,有如下的三種:
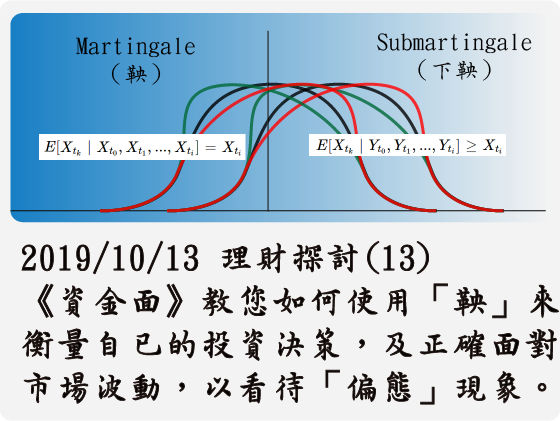
`E[X_(t_k)|X_(t_0),X_(t_1),...,X_(t_i)]=X_(t_i)`,`{X_(t_i)}_{i=0}^oo`稱為 Martingale。
`E[X_(t_k)|X_(t_0),X_(t_1),...,X_(t_i)]<=X_(t_i)`,`{X_(t_i)}_{i=0}^oo`稱為 Supermartingale。
`E[X_(t_k)|X_(t_0),X_(t_1),...,X_(t_i)]>=X_(t_i)`,`{X_(t_i)}_{i=0}^oo`稱為 Submartingale。
其中,Martingale(鞅)具備公平的賭局,沒有任何趨勢,就好像投擲硬幣一般,不管是押正反兩面哪一邊,都沒有特別的優勢存在。而 Supermartingale(上鞅)不具備公平的賭局,有下跌的趨勢,就好比玩吃角子老虎機一樣,隨著玩的次數愈多,玩家剩餘的資金將愈少。而 Submartingale(下鞅)則具有贏過莊家優勢的賭局,有上漲的趨勢,不過這樣的賭局通常出現在市場沒有效率、稀缺或金融市場恐慌的時候。因此,投資股票要能長期達到正報酬,就是要確保我們的投資決策具有 Submartingale(下鞅)的趨勢,也就是隨著參與的次數越來越多,隨著時間的推移,讓本金具有長期上漲的趨勢。然而,不同的投資者,不同的投資策略,都會產生不同的 Martingale(鞅)。
(投資本金於三種「鞅」的趨勢線,自行繪製。)
報酬率結合「鞅」的概念
假設`W_(tn)`是資產 W 從時間 0→t 的累積報酬率,`Delta t`代表單位時間,則`Delta W_t=W_(t+Delta t)-W_t`,因此累積報酬率`W_(tn)`可以表示為多個時間軸的報酬率總和,如下:
`W_(t_n)=W_0+sum_(k=0)^(n-1)Delta W_(t_k)`
由於每個報酬率`Delta W_(t_k)`符合常態分布`Delta W_(t_k)~N(0,Delta t)`,且相互獨立,因此累積報酬率的分布是`Delta W_(t_k)~N(0,t_n=n Delta t)`,繪圖如下。
(報酬率的常態分布,自行繪製。)
投資報酬率結合「鞅」之後,關鍵處就在平均值 `mu` 所在的位置,到底是出現在 0 軸的左邊、抑或是 0 軸的右邊,當:
(1)`mu=0`,投資活動不影響本金的增加或減損。
(2)`mu<0`,投資活動影響本金呈現下跌趨勢。
(3)`mu>0`,投資活動影響本金呈現上漲趨勢。
(`mu`的左移及右移影響報酬率的常態分布位置,自行繪製。)
在機率的概念裡,過去發生的事稱為平均值(`mu`);而未來還未發生,但預期可能發生的結果便叫做期望值。因此,平均值是我們依據過去的經驗所產生的結果均值;而期望值便是我們維持過去相同行為模式下,預期可能達到的未來結果的期望。
期望值 vs 條件期望值
過去筆者的文章曾舉例,如果有一個投擲硬幣的實驗 且硬幣正面(贏錢)的機率較高、反面(賠錢)的機率較低,則這枚硬幣就稱為具有正期望值的賭局,在「鞅」的概念裡,稱為 Submartingale(下鞅)。可惜的是,一個具有正期望值的賭局通常是不存在、或非常少數而稀有,由於遊戲的創造來自莊家,莊家不會創造出對自己不利,或讓自己虧損的規則。而玩家所參與及接觸的,通常由別人創造,因此幾乎絕大部分都是負期望值的賭局。
因此,投資人最關心的事,便是如何將投資達到正期望值。以 21 點為例,由於遊戲規則對莊家有利,對玩家則是負期望值。但是在一個賭局裡,撲克牌可以重現的點數為有限個(使用固定數量的牌組),因此在玩家參與的賭局下,勝率並非一個純粹固定機率的概念,而是一個排列組合下產生的變動機率。因此,算牌的玩家,可以透過牌局裡已出現的點數、及未出現的點數,來計算剩餘排列組合下,少數出現對玩家有利的機會,這些透過計算,可以達到正期望值的機會,長期平均報酬便稱為條件期望值。
在股市裡,也具備某種條件下可以達到的正期望值賭局。最普遍的例子就是,存股達人們買進好公司且長期持有下,好公司透過公司良善的經營,並長期正向發展及回饋股東,自然產生「正期望值」的股價變化或股息收入。而這個產生正期望值,是具有條件篩選,透過條件而達到「正期望值」的結果,我們就稱之為是個具有「正條件期望值」的賭局。因此,我們可以看到一個現象,若說一個投資者眼光好,可以買到上漲的股票,其實並不是他真的眼光好,而是他設定了參與「正期望值」的進場條件,以下便舉幾個例子來說明:
1、「存股」帶的條件是買進「好公司」。
2、「價值型投資」帶的條件則是買進「低價」。
3、「成長型投資」帶的條件則是買進「成長」。
4、「題材型投資」帶的條件則是買進「上漲題材」。
5、「技術型投資」帶的條件則是買進過去價格(量與價)變化產生正向次數較多的「型態」。
6、「籌碼型投資」帶的條件則是買進「大戶正在買的股票」。
7、「ETF型投資」帶的條件則是買進「權值最大 50 家公司」(0050)或「高殖利率 50 家公司」(0056)。
以數學來定義條件期望值,當 `{W_(t_i)}_(i=0)^oo` 和 `{W_t>=0}` 兩條件成立,且都是隨機過程時。以隨機變數 X 與 Y,定義為「股價」及「資訊量」的關係,則條件期望值可以表示如下:
`E[X|Y=y]=int x f_(X|Y)(x|y)dx=int x frac{f_(X,Y)(x,y)}{f_Y(y)}=g(y)`
多條件期望值下的「鞅」
當上節的條件機率具有隨機變數 X,及多個資訊流`{Y_(t_1),Y_(t_2),...,Y_(t_i)}`時,可得到多條件式期望值`E[X|Y_(t_1),Y_(t_2),...,Y_(t_i)]`。由於隨機變數 X 可表示為 `{X_(t_k)}_(k=0)^oo`,且對應於 `{Y_(t_i)}_(k=0)^oo` 的隨機變數有`{X_(t_i)}_(k=0)^oo`,其中 `0<=t_i<=t_k` ,因此可表示成一個 Markov 形式的條件期望值,且存在一函數 h 如下:
`E[h(X_(t_k)|Y_(t_0),Y_(t_1),...,Y_(t_i)]=E[h(X_(t_k))|Y_(t_i)]`
因此在多條件機率下,「鞅」具有如下的三種形式:
`E[X_(t_k)|Y_(t_0),Y_(t_1),...,Y_(t_i)]=X_(t_i)`,`{X_(t_i)}_(i=0)^oo`是一個 Martingale。
`E[X_(t_k)|Y_(t_0),Y_(t_1),...,Y_(t_i)]<=X_(t_i)`,`{X_(t_i)}_(i=0)^oo`是一個 Supermartingale。
`E[X_(t_k)|Y_(t_0),Y_(t_1),...,Y_(t_i)]>=X_(t_i)`,`{X_(t_i)}_(i=0)^oo`是一個 Submartingale。。
(使用多條件機率下的股價常態分佈,自行繪製。)
現實情況下的偏態現象
再來談一種偏態現象,代表機率分佈的峰值中位數與平均值不對等,即左右邊的形態不對稱。本文前述所討論的「長期報酬率」呈現一種常態分佈,是指在長期取得不同樣本數的情況下產生。但是,短期報酬的實際面貌,卻容易受到外在情勢的影響,造成偏態分佈的情況。因此,筆者提出三種外在情勢的改變,所造成的偏態如下圖。
1、負偏態分佈(negatively skewed distribution):外部情勢看多、投資人獲利偏好。
2、正偏態分佈(right skewed distribution):外部情勢看空、投資人風險偏好。
2、正態分佈(normal distribution):外部情勢中性、個股表現為主。
(在不同外部情勢下造成的偏態現象,自行繪製。)
在偏態下,短期績效好壞來自市場波動
從上一節的偏態現象,我們可以看出,短期績效(報酬率)的好壞主要來自外部情勢的干擾,來自大多數投資人信心程度的高低。信心高則股市呈現負偏態分佈(高估企業獲利),反之信心低則呈現正偏態分佈(低估企業獲利)。由於短期績效,來自市場情勢的隨機變動影響最大(如政治情勢、環境與政策、消息面等),因此只有看短時間的績效無法評斷投資人功力的好壞,但是長期則回歸均值的表現。也就是說,可以將金融的世界視為一種隨機混沌的機制,但是卻可以從中透過一些規則(即條件期望值大於市場期望值),來達到優於市場平均報酬,即打敗市場的一些方法。但可惜的是,若評估的時間太短,市場非常容易受到外部情勢的干擾,再好的方法都打不過市場的快速變動,而影響整體統計的結果。因此,由於市場的扭曲,容易造成投資者因短期的成功案例而高估自已投資能力,後續因相同策略方法而抬出市場的投資人大有人在。因此我們需要非常的了解,股市是個非常容易受到干擾的市場,且偏態的現象是個長期存在的干擾,影響我們對於結果的判斷,改變我們的心理預期。
由於偏態現象時常直接決定我們短期投資結果,因此大多投資者很容易被說服:在外部情勢不好時減碼、情勢好時加碼。但是,對於筆者而言,外部情勢的變動,產生變動的因素太過複雜,並不容易預測,就好比猜投擲硬幣或丟骰子的結果一般。比方說,假如您看到一枚硬幣已連續丟出了 5 個正面,你會如何去猜測下一次出現正面或反面呢?也許你會認為這枚硬幣不是公正的硬幣而猜下一次同樣是正面,也有另一群人會猜已經出現 5 次正面,下一次總該出現反面了吧?若以技術分析來看,看對的準確率也同樣來自機率問題。因此,在筆者的觀念裡,假如您已經找到一個模式可以讓條件期望值高於市場期望值,也就是您已經習慣從 21 點上透過算牌來獲利,就不太必要再去猜測外部丟硬幣或丟骰子的結果。因為在小樣本的情況下,很難去判斷猜對了幾次市場的走勢,到底來自運氣還是來自實力。也就是,直接把不確定性視為一種雜訊與干擾,而去掌握自已可以掌握的部份,才是筆者長期秉持的理念。
忽略偏態效應,長期回歸均值
偏態在數學裡也有個特色,也就是當樣品數夠多時,最終趨勢會朝向常態分佈發展。如 M 型化社會就是個很明顯的偏態現象,資產階級及無資產階級,長期朝向兩個不同方向發展,就形成一個 "M 型分佈",但 M 型化社會的偏態分佈是否會回歸常態分佈呢?歷史上的例子,最終的下場都來自於戰爭跟改朝換代,當經濟比較差(正偏態分佈)的一方已經活不下去時,經濟比較好(負偏態分佈)的一方麻煩就大了。因為國家一旦走向毀滅與革命,經濟好的家庭常常成為戰場底下的獵物,而快速回歸常態分佈。而在投資裡,股災的發生是個正偏態分佈,但如巴菲特的危機入市理論,在正偏態的時點進入,往往最終是享受「回歸常態分佈」的贏家。相反的,在股市熱絡時進場(負偏態的時點進入),若個股的股價皆已被高估,則最終勢必要成為「回歸常態分佈」的輸家。
小結
在本文裡,筆者探討到兩個概念,一個是「鞅」,另一個是「偏態」。而本文為了嚴謹的定義這兩個「數學概念」,因此有一點點數學成份,但讀者可以略過,直接感受一下兩個結論。在「鞅」的概念裡,報酬率能否打敗大盤可以透過「條件式」選股來達成,使投資成為一個「有利賭局」,不管您的方式是「存股」、「價值型投資」、「成長型投資」、「題材型投資」、「技術型投資」、「籌碼型投資」抑或「買進 ETF」等,都可以透過條件式的進場,來達到「條件期望值」大於「市場期望值」的結果(即勝過市場)。但「偏態」的現象,卻是我們較難以掌握的部份,卻重大影響短期投資績效。因此,你可以像筆者一樣忽略「偏態」的影響,也可以透過賽局理論來猜測後市的可能結果,去賭機率較大的部份,但是由於去猜測後市的結果,於統計樣本數上遠遠不如個股來得多,在「小數法則」下很容易產生「生存者偏誤」的謬誤,這點對於想要猜測後市的投資人,風險也要有所認知。由於筆者是個理科人,對於投資理念有比較多來自於「數據科學」等要求,但筆者也並非固執的投資人,會因觀察到的現象而做調整,但也因重視「大數法則」,因此也不太在意單一「個案」的探討,但卻重視「市場」的趨勢。因此,本文主要在談筆者的一點心得與觀念,套用在個股與市況上,絕對不一定正確(因為一個機率的問題,最終的結果仍是個機率),至於受不受用就請讀者自行斟酌吧。
※本文為個人研究,非投資建議,相關數據依據當時公布之財報資料推估,僅供讀者參考。

資金面

































0 意見:
張貼留言